::: Sicherheitsmaßnahmen GELD :::

[Marc of Frankfurt]

Die Sexualität des Geldes:

Wie sich das Geld vermehrt und das Rechnen mit Google


Für richtige Geldfragen ist der normale Taschenrechner zu dumm, denn er kann nur die Grundrechenarten (+-*/%). Da nicht jeder einen Rechner für Finanzmathe oder Ingenieure hat, hilft Google

Google ist potenter. Google kann auch x^y = z z.B. x³ = z also potenzieren und die 2(!) Umkehrungen wurzelziehen und logarithmieren:

Bei diesen Formeln mit x, y, z gibt es immer 3 verschiedene Berechnungen:
z = x^y . . . . . (x hoch y = x * x * x... y-mal)
x = z?y . . . . . (y. Wurzel aus z)
y = log z / log x (Logaritmus)

Bsp. ausrechen mit Google:
3^2 . . . . . . . (3 hoch 2 = 9) - Ergebnis vom Potenzieren 3² = z?
2th root of 9 . . (Quadratwurzel aus 9 = 3) - Wie groß ist die Basis (Grundzahl) von x² = 9?
log 9/log 3 . . . (Logarithmus von 9 durch Logarithmus von 3 = 2) - Wie groß ist der Exponent? Oder wie oft muß 3 multipliziert werden damit 9 rauskommt?
Formel einfach in die Google-Zeile im Browser eingeben
http://google.about.com/od/googlepowers ... atorqt.htm





Zeitformeln für unser Geld:

• "Geld ist eine Hure die niemals schläft,
  wenn du nicht auf sie aufpaßt, ist sie eines Tages weg."
  
  --Gordon Gecko in Wall Street II, 2010

1. Verzinsung d.h. Wertsteigerung von einem Einmalbetrag ausrechnen
(Zinseszinsrechnung)

Wieviel ist mein heutiger Geldbetrag A wert nach n Jahren?
Wieviel Geld habe ich nach n Jahren bei p%?

Beispiel:
A Anfangskapital 1000 Euro
p Zinsatz 5% = 0,05
n Zeit in Jahren z.B. 6
E Endkapital in Euro
Für das Endkapital gilt die Formel:

• Endkapital E = A * (1+p)^n
  (Zinseszins-Formel)
  = 1000*(1+5%)^6
  = 1000*1,05^6
  = google.de/search?q=1000*1,05^6
  = http://tinyurl.com/3by4jaa
  = www.google.de/search?q=1000*1,05^6
  [die vollständige google-Zeile muß rüberkopiert werden]

Einfach mit deinen Zahlen überschreiben um Varianten zu rechnen...

[1+p = 1,05; Google setzt 1,05^6 in Klammern um anzuzeigen dass gilt: exponenzieren vor multiplizieren vor addieren. Wenn man die Gleichung verändert muß man also evt. anders Klammern setzen.]

Wer also sein Geld unter dem Kopfkissen sammelt, hat nach n Jahren nur das Anfangskapital 1000 Euro oder nur die aufsummierten zurückgelegten Sparbeträge nach 6 Jahren. Wer es aber z.B. zur Bank auf den Geldmarkt bringt d.h. INVESTIERT hat in diesem Beispiel allein von einer einzelnen Einzahlung schon ein Drittel mehr! Das ist die Magie des Zinseszins, also das Wachstum durch regelmäßige Zinszahlung auf stehenbleibende Zinseinkünfte (Thesaurierung, Schatzbildung).

Das ist einer der Hauptvorteile von legalem, versteuertem, weißen Geld im Gegensatz zu Schwarzarbeit in einer Schattenwirtschaft.





Dasselbe Wachstums-Gesetz gilt auch für Schulden! Wer also seine Handyrechnung, Miete, Blockschulden oder Steuern nicht bezahlt (bezahlen kann), der hat wegen dem Zinseszins-Effekt in relativ wenigen Jahren ganz fürchterlich hohe Schulden und gerät in die Schuldenfalle (= moderner Schuldturm).





So unterschiedlich schnell wächst Geld:
Erst kaum merkbar, dann explodiert es! Deshalb früh anfangen und lange durchhalten!
Doppelter Zinssatz bedeutet MEHR als doppeltes Wachstum!



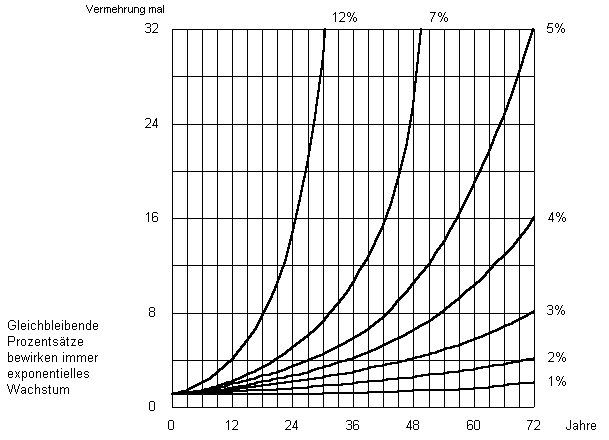
Aus dem epochalen Buch von Helmut Creutz, Geld Syndrom 1993.





Einen Schritt schwieriger wird die Rechnung, wenn man die Zeit d.h. die Jahre n wissen will, weil in der Zinseszins-Formel n als Hochzahl vorkommt (Exponent in der Exponentialfunktion, Potenzfunktion oder Wachstumsfunktion):

Beispiel: 3^n = 9,5
("3 hoch n gleich 9,5")

Frage: Wie groß ist n?
("Wie groß ist der Exponent n ?")

Lösungsweg:
ln(3^n) = ln(9,5) Gleichung auf beiden Seiten Logarithmiert
(Logarithmieren ist eine Umkehrung von Exponenzieren).
n * ln(3) = ln (9,5) [Logaritmusumformungsregeln:
inneres Produkt wird äußere Summe,
innerer Exponenten, als Faktor nach vorne heraus holen.]
n freistellen durch Division auf beiden Seiten.

Lösung:
n = ln 9,5/ ln 3
= google.de/search?q=ln 9,5/ln 3
= www.google.de/search?q=ln%209,5/ln%203
= http://tinyurl.com/6w6jqpx





Fortsetzung zum Geldanlage-Beispiel:
Um die Jahre n (Anlagedauer, Haltezeit) oder den Zinssatz p zu berechnen die Formel umstellen:
E = A * (1+p)^n ("Zinseszins-Formel")
lnB = ln[A * (1+p)^n] = lnA + ln[(1+p)^n] = lnA + n * ln(1+p)

Beispiel wie oben:
A Anfangskapital 1000
E Endkapital 1249
p Zinssatz 5% = 0,05
n Jahre 6

Wie lange muß ich Geld fest anlegen?
Wie hoch muß der Zinssatz sein?

Lösungen:

• Anlagedauer n in Jahren
  = (ln E - ln A) / ln (1+p)
  = (ln 1340 -ln 1000) / ln 1,05)
  = google.de/search?q=(ln 1340 -ln 1000) / ln 1,05)
  = http://tinyurl.com/6bgr3m5
  
  Zinssatz p
  = e^((ln E - ln A)/ n) - 1
  = e^((ln 1340 - ln 1000)/6)-1
  = google.de/search?q=e^((ln 1340-ln 1000)/6)-1
  = http://tinyurl.com/7dx9fx6

2. Rente d.h. regelmäßige Zahlungen ausrechnen
(Rentenrechnung)

(Hier folgt die sog. mathematische Rentenberechnung für private Kapitalanleger.
Die Berechnung der sog. gesetzlichen Rente steht hier.)

Es gibt zwei Phasen der Kapitalanlage:
2.1 Einzahlung (Sparplan)
2.2 Auszahlung (Rente)

Damit ein ideales Geschäftsmodell für das (Sexworker-)Arbeitsleben funktioniert muß gelten:

• Endwert E der Ansparphase = Barwert B der Auszahlungsphase

2.1 Einzahlung d.h. Kapitalanlage-Sparplan ausrechnen
(Investitionsphase)

Fragestellung als Sexworker der investieren will für die Zukunft:
Wieviel muß ich bei der Arbeit jährlich einzahlen (Einzahlungsrate r pro Jahr), um nach n Jahren ein bestimmtes Kapital E zu haben?
(Endwert-Berechnung)

Beispiel:
p Zinssatz 5% = 0,05
q Aufzinsfaktor = 1+p = 1,05
n Jahre 10
[durchschnittliche Arbeitszeit eines Sexworkers]
r Rateneinzahlung pro Jahr = 350 Euro pro Monat * 12 Monate = 4.200 Euro pro Jahr
[das entspricht der durchschnittlichen Renteneinzahlung bei Angestellten ohne extra zu Sparen]
E Endwert (Wert aller Einzahlungen)

Lösung:
Wert am Ende aller Einzahlungsraten:

• Endwert E = r (q^n -1) / (q-1)
  = 4200 (1,05^10 -1) / (1,05-1)
  = google.de/search?q=4200(1,05^10-1)/(1,05-1)
  = http://tinyurl.com/63d2jlq
  = über 50.000 Euro

Vgl.: 4.200 Euro/Jahr * 10 Jahre = 42.000 Euro
d.h. 20% zu wenig beim Sparen im Bankschließfach oder Matratze.
Oder 42.000 + 5% Zins = 4.200*10*1,05=44.100
immer noch 17% fehlerhaft bei zu einfacher, falscher Formel.

Umgestellte Formeln:
Wie lange muß ich sparen?
Welche Jahresraten sind notwendig?
Wie muß das Geld verzinst werden?

• Anlagedauer n in Jahren
  = log ((E (q-1) /r) +1) / log q
  = log ((50.000(1,05-1)/4.200)+1) / log 1,05
  = google.de/search?q=log ((50000(1,05-1)/4200)%2B1) / log 1,05
  = http://tinyurl.com/7qp6u4g
  = 9,57 Jahre
  
  50.000 Euro / 4.200 Euro/Jahr = 11,9 Jahre
  (20% Abweichung bei falscher Rechenmethode)
  
  Rate r pro Jahr
  = E(q-1)/(q^n -1)
  = 50.000(1,05-1)/(1,05^10 -1)
  = google.de/search?q=50.000(1,05-1)/(1,05^10 -1)
  = http://tinyurl.com/86ernt7
  
  Effektiver Zinssatz p in % = ...

Was bei 1. der Zinseszinsberechnung das Anfangskapital A genannt wurde, heißt hier bei 2. der Rentenberechnung der Barwert B!
Nachschüssige Rente wie hier verwendet heißt die Zahlungen erfolgt rechnerisch jeweils am Ende des Jahres.
Die Renten-Formeln:
http://de.wikipedia.org/wiki/Rentenrechnung




Symbolphoto: Barwert einer Rente, d.h. Endwert der Sparphase vor Verrentung des Kapitals am Rentenbegin.

1 Million Euro in 500 Euro Scheinen gestapelt sind 12 cm hoch. Als Barwert ergäbe 1 Mio bei 5% Zinseszins angelegt und verrentet ein Leben lang (79,8 Jahre) eine monatliche Rente in Euro in der Höhe der ersten Zahl in der bei der Google-Suche eingegebenen Formel: http://tinyurl.com/6m44qjp (Der Google Rechner zeigt das Endergebnis ca. 1 Million und man kann die verschiedenen Eingabewerte (Jahresrate, Prozentwert, Jahre) in der Formel ändern, um schrittweise dem Ergebnis näher zu kommen = Iteratives Lösungsverfahren durch Ausprobieren.)



2.2 Rentenhöhe d.h. Verrentung der Kapitalanlage ausrechnen
(Rentenphase)

Fragestellung als Rentner der leben und konsumieren will:
Wie hoch muß das angesparte Kapital B bei Rentenbeginn sein, damit es mir jährlich eine Rente (Auszahlungsrate r pro Jahr) auszahlen kann?
(Barwert-Berechnung)

Beispiel:
n Jahre = Lebenserwartung - Renteneintrittsalter = 80 - 65 = 15
[Sexarbeit endet oft mit 30...45 Jahren, d.h. n wäre 35...50]
r Rentenauszahlungs-Rate pro Jahr = Lebenshaltungskosten pro Jahr im Alter = 1.500 Euro/Monat * 12 = 18.000 Euro/Jahr
[Zimmer im Pflegeheim mit Vollversorgung kostet aber mind. 4.000/m also 48.000/a]

Lösung:
B Barwert (Wert der Rente am Rentenbeginn):

• Barwert B = r (q^n -1) / q^n (q-1)
  = 18.000 (1,05^15 -1) / (1,05^15 (1,05-1))
  = google.de/search?q=18000(1,05^15-1)/(1,05^15(1,05-1))
  = http://tinyurl.com/3l47y7f

Also ist in dem ausgerechneten Beispiel der benötigte Barwert B der gewünschten Rente um den Faktor 3,5 mal zu groß als der zuvor bereits angesparte Kapitalwert E. D.h. es reicht nicht für eine ausreichende, sofortige Rente nach der Sexarbeit. Deshalb zuerst 2.2 und dann 2.1 ausrechnen. Aber zumindst ist es ein guter Kapitalstock für einen Neuanfang z.B. Geschäftsneugründung www.sexworker.at/exit





Da viele Sexworker
- nur wenige Jahre (viel) verdienen können
- diskret, geheim d.h. schwarz arbeiten
- nur gelegentlich arbeiten (können)
- nur für den eigenen derzeitigen Lebensunterhalt arbeiten (= Überlebenssexualität)
- nie auf Dauer soviel arbeiten können wie ein festangestellter Sacharbeiter ("Kein Beruf wie jeder andere")
- nicht genau gelernt bekommen haben wie man richtig rechnen muß (Sexworker Academy fehlt, Tabu der Förderung von Prostitution)
- kein Arbeitgeber etwas für sie in die Sozialversicherung einbezahlt (ProstG gescheitert, Zuhälterverdikt)
laufen viele Sexworker in eine existenzbedrohende Falle und werden später zum Sozialhilfefall (Altersarmut).

Das eigene innere Coming-out als professioneller Sexworker und die Legalisierung der Sexarbeit sind also eine Grundvoraussetzung, um überhaupt nachhaltig erfolgreich sein zu können (Legalisierunsworkshops, Einstiegsberatung, Coming-out Gruppen und berufsbegleitende Erwachsenenfortbildungen benötigen die Sexworker dazu als Unterstützung, um die strukturelle Prekarisierung in der Prostitution überwinden zu können).
Legalisierung nicht nur auf der öffentlich-gesellschaftlichen-politischen Ebene, sondern zunächst viel wichtiger auf der privat-steuerrechtlich-versicherungstechnischen Ebene!!! Hier bleibt jeder prekärbeschäftigte, alleinselbstständige Solo-Sexworker sich weitgehend selbst überlassen.

Zeit ist Geld

Carpe Diem




___
Faustformel um abstrakte "Zinssätze (Prozentwerte)" in anschauliche "Verdopplungszeiten (Jahre)" umzurechnen (72er-Regel):
www.sexworker.at/phpBB2/viewtopic.php?p=66646#66646 (SW-only)

Wer mehrere Rechnungen vergleichen und sichern will oder wer mehre Zahlungen also eine Zeit-Reihe wie bei der Rente ausrechnen will, benutzt am besten eine Tabellenkalkulation vom Office-Paket oder on-line. Dort sind einerseits alle Funktionen inkl. Erklärung und Eingabebeispiel bereits eingebaut oder man kann andererseits für jede Jahreszahlung (Rate) ein eigenes Tabellenfeld mit Formel machen und so auf indirektem Weg ohne komplizierte Gesamt-Formel zum Ergebnis kommen (schrittweises Rechnen, Iteration).



Rechenformulare als Beispielrechnung

Deutsch
Anschauen https://docs.google.com/spreadsheet/ccc ... html&gid=0
Rechnen https://docs.google.com/spreadsheet/ccc ... 0c3b1I3a1E
( www.bit.ly/sexworkerccc - Sexworker collaborate cloud computing - gemeinsame on-line Rechenblätter)

English https://docs.google.com/spreadsheet/ccc ... tml&gid=41
( www.bit.ly/sexworkerinternet )

www.de.wikipedia.org/wiki/Zinseszins
www.de.wikipedia.org/wiki/Formelsammlun ... nzahlungen
www.googleGuide.com/calculator.html

Englische terminology:
http://en.wikipedia.org/wiki/Compound_interest
http://en.wikipedia.org/wiki/Amortization_calculator
http://en.wikipedia.org/wiki/Annuity_%2 ... _theory%29
http://en.wikipedia.org/wiki/Time_value_of_money

SW-only:
Geld verdienen: www.sexworker.at/phpBB2/viewtopic.php?t=1588
Geld anlegen: www.sexworker.at/phpBB2/viewtopic.php?t=1312





Direktlink bitte weitergeben:
www.sexworker.at/phpBB2/viewtopic.php?t=5319&start=33

[Marc of Frankfurt]

Was für Kosten hat die allein-selbstständige Sexarbeiter_in:

Kosten-Vergleichs-Tabelle


Ausgaben in EUR im Monat (ohne Eigenverdienst)

1.) Betriebskosten
. . . . . . . . . . . . . . Bordell .Nachtclub .Apartment . . Straße
Miete . . . . . . . . . . . . 4.500 . . . .750 . . .2.000 . entfällt
Nebenkosten (Essen, Wäsche) . 1.800 . entfällt . entfällt . entfällt
Werbung . . . . . . . . . .entfällt . entfällt . . .1.000 . entfällt
Kondome . . . . . . . . . . . . .60 . entfällt . . . . 60 . . . . 60
Schwämmchen . . . . . . . . . . .10 . . . . 10 . . . . 10 . . . . 10
Gleitgel. . . . . . . . . . . . .20 . . . . 20 . . . . 20 . . . . 20
Massageöl . . . . . . . . . . . .30 . entfällt . . . . 30 . . . . 30
Papierrollen. . . . . . . . . . .50 . entfällt . . . . 50 . . . . 50
Fahrtkosten . . . . . . . . . . . . . . . .600 . entfällt . . . .600
Arbeitskleidung . . . . . . . . 150 . . . .150 . . . .150 . . . .100
Pauschale . . . . . . . . .entfällt . . . .300 . entfällt . entfällt
Putzfrau/Telefonistin . . .entfällt . entfällt . . .2.500 . entfällt
Telefon . . . . . . . . . .entfällt . entfällt . . . .500 . entfällt

Gesamtsumme pro Monat . . . . 6.620 . . .1.830 . . .6.320 . . . .870
Gesamtsumme pro Tag (30 Tage) . 220 . . . . 83 . . . .210 . . . . 29
Kostenfalle Blockschulden im Bordell:
www.sexworker.at/phpBB2/viewtopic.php?p=88560#88560
Schutzgeld an Zuhälter auf der Straße:
www.sexworker.at/phpBB2/viewtopic.php?p=115000#115000


2.) Private Kosten:
Krankenversicherung (Pflicht) . 300 . . . .300 . . . .300 . . . .300
Rentenversicherung. . . . . . . 100 . . . .100 . . . .100 . . . .100
Unfallversicherung. . . . . . . 100 . . . .100 . . . .100 . . . .100


3.) Steuern:
Einnahmen-Überschuß-Rechnung (EÜR) und Berechnung der Steuern:
www.sexworker.at/phpBB2/viewtopic.php?p=98575#98575

Steuerschätzung FA München rückwirkend für 3 Jahre ergibt 90.000 EUR Steuernachzahlung:
www.sexworker.at/phpBB2/viewtopic.php?p=52070#52070

(Alle Angaben als Beispiel vom SW Seminar und ohne Gewähr)





.

[Aoife]

Ein sehr interessanter Artikel von Michael Hudson, ehemaliger Wall Street Ökonom, jetzt Professor an der University of Missouri, Kansas City, kommt zu folgendem Schluß:

"Den Euro retten" ist ein beschönigender Ausdruck der Regierungen für das Retten der Kapitalistenklasse - und damit einer Schuldendynamik, die sich ohnehin dem Zusammenbruch nähert, egal was sie tun."

Ganzer Atrikel: http://rebel-alliance.org/2011/05/28/br ... nterpunch/

Liebe Grüße, Aoife

[Marc of Frankfurt]

Sexarbeiter sind gar keine Arbeiter...


...zumindest was das Geld und die Finanz- & Steuer-Kalkulation betrifft:

Arbeitern zahlt der Unternehmer ein Bruttogehalt (Arbeitgeberbrutto, zusätzlich Sozialabgaben-Unternehmeranteil und die Kosten für den Arbeitsplatz).

Vom Brutto-Einkommen des Arbeiters gehen Sozialabgaben (Arbeitnehmeranteil) und Einkommensteuer ab und er erhält am Ende ein Nettogehalt.

Der Sexarbeiter ist aber Unternehmer (Kapitalist) !!!
Unternehmer seiner selbst !!!
Wir müssen alles selbst bezahlen und allein erwirtschaften.





So kalkulieren Sexworker-Alleinunternehmer_innen
In 2 Stufen: zuerst Betrieb, dann Privatperson (hier ein Beispiel mit Zahlen):

Einnahmen (Brutto Umsatz als Unternehmen)

- Umsatzsteuer (Vorsteuer, 19%, entfällt beim Kleinunternehmer)
_______________________________
= Netto Umsatz
===============================

- Betriebsausgaben (Kosten für den Arbeitsplatz s.o. ca. 1/3 oder 33% vom Umsatz)
_______________________________
= Betriebsergebnis (Gewinn)

- Gewerbesteuer (evt.)
- Sexsteuer (evt. kommunale Vergnügungssteuer)
- Vorsteuer (evt. tägliche Einkommensteuer nach Düsseldorfer Verfahren)
_______________________________
= Betriebsergebnis nach Steuern
===============================
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

= Bruttoeinkommen als Arbeiter_in/Unternehmer_in

- Krankenkasse (Pflicht)
- Sozialabgaben
- Sonderausgaben
- Freibeträge
_______________________________
= zu versteuernes Einkommen zvE

- Einkommensteuer (nach Steuertabelle z.B. 30% vom zvE)
_______________________________
= Nettoeinkommen
===============================

- Lebenshaltungskosten (Miete, Strom...)
- Rücklagen (wenn Auto/Waschmaschine kaputt gehen...)
- Schuldenrückzahlungen (falls das der Grund für den Einstieg in Sexwork war)
- Unterhaltszahlungen (Kinder, Eltern, remittance)
- Sparen für Eigentumswohnung, Ausstieg, Altersvorsorge (mind. 350 Euro/Monat)
_______________________________
= frei verfügbares Einkommen
===============================


Wer "Einnahmen = frei verfügbares Einkommen" oder brutto = netto rechnet,
betreibt Überlebenssexualität oder Hobbysexwork in einer gefährlichen rechtlichen Grauzone.

Dieses System früh und richtig für sich einzuführen erscheint erstmal nicht leicht und sogar schmerzhaft, wenn man jung und allein ist und viel Geld verdient d.h. hohe Steuern zahlen muß (Coming-out gegenüber Finanzamt, bezahlen trotz Stigmatisierung, Überforderung bzw. Verlockung zur Scharzarbeit).

Wenn man später einmal weniger verdient, gelingt einem die Umstellung auf richtige Kalkulation nur sehr sehr schwer (Legalisierungs-Hürde Steuernachzahlung). Die Prostitution kann so zur Falle werden (Geheimprostitution = illegale Prostitution, Razzia/Steuerfahndung (verpfiffen, erpresst und geschätzt zu werden), Ausstiegshürde Steuernachzahlung, versäumte Teilnahme am frühzeitigen, legalen d.h. gut verzinsten Kapitalaufbau s.o. und Altersarmut bzw. Sozialhilfe drohen).





Steuerinfos für Sexworker in Deutschland:
www.sexworker.at/phpBB2/viewtopic.php?p=29178#29178

Kalkulationen für Sexworker in Österreich:
www.sexworker.at/phpBB2/viewtopic.php?p=40548#40548
www.sexworker.at/phpBB2/viewtopic.php?p=40546#40546

Legalisierungsmerkblatt für Migrant_innen in Deutschland:
www.sexworker.at/phpBB2/viewtopic.php?p=9213#9213

So kalkulieren die migrantischen Sexarbeiter im Frankfurter Laufhaus:
www.sexworker.at/phpBB2/viewtopic.php?p=39273#39273 SW-only





.

[Marc of Frankfurt]

Zahlen mit EC-Karte macht dick

Je abstrakter der Bezahlvorgang sei, desto schwerer sei es, vor der Kasse deponierten Lockwaren wie Schokoriegeln zu widerstehen. Bei einer Karten-Zahlung landen bis zu 70% mehr Dickmacher auf dem Band.

Wer abnehmen will, sollte also bar bezahlen, so wie es beim sportlichen Sexwork immer schon üblich ist ;-)

www.ksta.de/html/artikel/1307782590731.shtml





Vermögende investieren verstärkt in Sachwerte

60% vermögende Anleger setzen einer Studie der Liechtensteiner Investmentgesellschaft Valluga zufolge bei der Geldanlage zunehmend auf Immobilien, Gold und Rohstoffe.

(Der Studie zufolge wächst das Vermögen der Reichen (+8%) bereits seit Jahrzehnten 3x schneller als die Volkswirtschaften insgesamt. Ca. 1 Millionen Millionäre im Deutschsprachigen Raum).

www.check24.de/news/finanzen-allgemein/ ... rte-41860/


Landgrabbing:

Harvard, Vanderbilt und andere führende US-Universitäten und private Stiftungs-Fonds benutzen britische Hedgefonds und europäische Finanzspekulanten wie Emergent Asset Management, um riesige Flächen afrikanischen Agrarlandes zu kaufen oder zu pachten bei Renditeerwartungen um 25%.

„Diese Unternehmen haben ein komplexes Geflecht von Firmen und Tochterunternehmen geschaffen, um sich schwache Aufsichtsbehörden vom Leib zu halten [organisierte Verantwortungslosigkeit]. Eine Analyse der Verträge enthüllt, dass viele dieser Geschäfte kaum Arbeitsplätze schaffen und Tausende von Menschen von ihrem Land vertreiben werden", sagte Anuradha Mittal, Director vom Kalifornischen www.oaklandInstitute.org.

Studien der Weltbank und anderen Institutionen deuten darauf hin, dass in den vergangenen 3 Jahren fast 60 Millionen Hektar –ein Gebiet von der Größe Frankreichs– von ausländischen Firmen in Afrika gekauft oder gepachtet worden sind.

"Dies schafft eine Unsicherheit im internationalen Nahrungsmittelsystem, die für die globale Sicherheit eine viel größere Bedrohung darstellen könnte als der Terrorismus."

E www.guardian.co.uk/world/2011/jun/08/us ... -land-grab
D http://principiis-obsta.blogspot.com/20 ... scher.html


Diese vertriebenen Leute kommen dann irgendwann als undokumentierte, ausbeutbare Sexworker, Farmarbeiter und Boatpeople bei uns in Europa an...


In Europa ist der Prozess der Landnahme durch den Adel seit dem Mittelalter dokumentiert. Enclosure Movement (Gentrifizierung):
http://de.wikipedia.org/wiki/Enclosure_Movement
http://en.wikipedia.org/wiki/Highland_Clearances

Das Gegenmodell ist die Allmende-Ökonomie (öffentlicher Güter)
vgl. Nobelpreis von Elinor Ostrom 2009:
www.sexworker.at/phpBB2/viewtopic.php?p=67365#67365

Thirana Deklaration zu Land Access:
www.landcoalition.org/about-us/aom2011/ ... eclaration





.

[Marc of Frankfurt]

Das was Arbeiter in den U.S.A. nicht bekommen, bekommen Sexworker bei uns auch nicht:

- bezahlter freier Wochentag
- bezahlter Jahresurlaub
- bezahlter Elternurlaub
- ...


Amerikanern und einigen anderen Ländern ergeht es wie soloselbstständigen Sexarbeiter_innen (in der Karte in rot wie Rotlichtbezirke).

Bezahlter Jahresurlaub (eine von 3 Karten):

Mehr: theSocietyPages.org


Allein diese drei nichtvorhandenen geldwerten Sozialleistungen (Sonntag, Urlaub, Mutterschutz) summieren sich auf einen Wertverlußt von ca. 14% + 8% + 7% = 29%. Der Gesamtwert der gesetzlich garantierten und entlohnten freien Tage, die bei uns die Gewerkschaften erkämpft haben, beträgt fast ein Drittel.

Ein Arbeiter in den U.S.A. und ein alleinselbstständiger Sexworker in A - CH - D im Sexworker.at-Land verdienen also ca. ein Drittel weniger (geldwerte Leistungen = bezahlte Freizeit) als ein Festangestellter im Regelarbeitsverhältnis.

Hier noch nicht berücksichtigt: Lohnfortzahlung im Krankheitsfall und bei Arbeitsunfähigkeit maximal 6 Wochen. Dafür wurde 1956 in Schleswig-Holstein 114 Tage lang gestreikt [Wikipedia].


Dieses Weniger an Sozialbeiträgen von Arbeitgeber bzw. Gesellschaft muß jeder AlleinSelbstständige also auszugleichen versuchen d.h. einpreisen in seine Stundenpreise.

Die manchen als ungerechtfertigt hoch erscheinenden Sexdienstleistungspreise müssen also dieses Drittel bereits enthalten, wenn man sich langfristig "nicht zu billig verkaufen" will !!!


Da aber die meisten Sexdienstleistungspreise de facto sehr niedrig sind und seit Jahren nur sinken (Nachfragermarkt, ehernes Lohngesetz), wird deutlich wie prekär die Lage der Branche und für viele Sexworker ist.

Manche Sexworker antworten auf dieses strukturelle Verdienst-Defizit instinktiv oder unbewußt mit Mehr- und Dauerarbeit d.h. Dauerbereitschaft z.B. Leben direkt im Bordell oder Dauer-Erreichbarkeit von Escorts und in der Wohnungsprostitution. Das ist eine sehr Burn-out gefährdende Arbeitsorganisation oder Tätigkeit (SWBO).





Wenn diese Betrachtung über Verdienst, Kosten und arbeitsfreie Zeit hilft durch eine kleine eigene Kalkulation von Einnahmen und Preisen einem ungesunden Arbeitsverhalten vorzubeugen, hat dieses Posting seinen Zweck erfüllt.





.

[Marc of Frankfurt]

Achtung

Betrugsgefahr bei internationaler Scheckzahlung


Ein gefälschter oder ungedeckter dem Sexworker persönlich ausgehändigter Scheck fällt spätestens beim Einlösen auf. Er platzt dann allerdings, wenn es bereits zu spät und die Sexdienstleistung längst erbracht ist.


Will man dem vorbeugen indem man sich bei einem internationalen Kundenkontakt die Scheckgutschrift schon vor dem Besuch gutschreiben läßt, so ist man dennoch NICHT abgesichert.

Denn ein gefälschter Scheck kann noch bis zu 1 Monat NACH der Zahlung auffallen und dann wird das Geld AUTOMATISCH vom Empfängerkonto wieder ZURÜCK GEBUCHT an die ursprünglich betrogene Bank.





Quelle aus England:

Everyone should know by now that paying by check, with the name and address of the recipient on it, is 100% scam !!! Even if the money clears in your account the whole amount will later be deducted from your bank account when the bank finds out it's stolen or forged.

You should all know that foreign cheques clear instantly but it takes about 1 month before the banks actually find out they are fake and later will deduct that money.

You should already be clued up about this !!! Never accept cheques !!! It will always lead you to being ripped off !!!


Vgl. Überweisungsbetrug:
http://de.wikipedia.org/wiki/%C3%9Cberweisungsbetrug

[Marc of Frankfurt]

Wie flexibel soll man/frau die Dienstleistungspreise reduzieren in der Krise, wenn kaum Kunden kommen?


Werbepsychologie & Preisforschung:

Sich nicht zu "billig verkaufen"


Statt rational abzuwägen, suchen die meisten Kunden vielmehr unbewusst nach Vergleichen, um abzuschätzen, ob sie sich etwas leisten wollen. "Was kostet heute ein anderes Vergnügen oder Produkt?" Über solche Denkmuster rechnet ein emotionaler Kunde sich den Preis plausibel.

Hier spielen Aufmachung, Marke, Atmosphäre und Image (softe Faktoren) eine entscheidende Rolle, um einen gehobenen Preis zu rechtfertigen, zu legitimieren.


Beim Wandel von der Industriegesellschaft zur Dienstleistungsgesellschaft, wird neben Preis und Produktwert die Kundenkommunikation immer wichtiger (Customer Relation Marketing). Der Markt in der Informationsgesellschaft wird vom Verkäufer- zum Käufermarkt (verstärkte Kundenmacht).


Nur der Typ Schnäppchen-Jäger checked Angebotslisten per Taschenrechner, läßt sich im Fachgeschäft beraten und kauft dann on-line (bezogen aufs Sexbiz: guckt Porno statt zu buchen)... Er ärgert sich dafür dann, wenn er wegen Fixierung auf den günstigsten Preis, auf (ausländischen) nachgemachten Billig-Schrott oder versteckte Kosten oder verfrühtes Nutzungsende reingefallen ist.


Die Aufspaltung der Kunden in Qualitäts-/Wert-Käufer (kauft trotz des Preises) und Billigpreis-Käufer (kauft wegen des Preises) zeigt sich auch in der Aufspaltung der Anbieter nach Spezial-Anbietern (Luxus, Escort, Massage, BDSM...) und Massen-Anbietern (Supermarkt, Laufhaus, FFK, Straße...). Ob je nach getroffener Grundsatzentscheidung der Umsatz = Preis x Absatz wirklich steigt, muß jeder selbst herausfinden und optimieren.

Ferner gibt es die Signalfunktion des Preises (sowohl nach oben als auch nach unten). D.h. der Preis muss alle komplexen Qualitätsinformationen von Produkt oder Dienstleistung vermitteln, die ein eiliger, uninformierter Konsumer anders nicht so schnell herausfinden kann.

Mit erhöhten Preisen können zudem viele nervigen oder unangenehmen Kunden abgeschreckt oder rausgefiltert werden. Weniger und hochpreisiger zu arbeiten kann angenehm sein, aber auch viel intensiver und fordernd anspruchsvoller (Mindfuck, Kulturkompetenz).


Für uns Verkäufer bestimmt sich der Preis keinesfalls primär nach der Kosten-Kalkulation (da sollte er natürlich mindestens drüber liegen, s.o. Deckungsbeitrag), sondern der Preis wird nach der Preis-Absatz-Funktion (PAF) bestimmt. D.h. der maximale Preis, den Kunden gerade noch zu bezahlen bereit sind, wird als Preis festgesetzt. Herausgefunden wird das mit Kundenbefragung, Mitbewerberanalyse und professionellen Marktforschungsmethoden wie z.B. Conjoint-Analyse.


Dann gibt es noch das grundsätzliche Problem des sinkenden Marktwertes in Abhängigkeit vom Lebensalter (siehe Bild in dem Posting). Sexworker dürfen ihre "Produktionsanlagen" aber nicht abschreiben und sind besonders herausgefordert andere Wege der Vorsorge zu finden, weil sie sonst unweigerlich in Altersarmut abrutschen (vgl. Ausstiegsproblematik www.sexworker.at/exit). Daher ist m.E. zu einem Gutteil auch das Prostitutionstabu begründet, weil dieses existentielle Problem so schwer individuell lösbar ist und so viele Sexworker scheitern und zum Sozialhilfefall werden.





Trix bei der Preisgestaltung sind:

- 49,85 statt 50,-- (oder im Sexbiz 69 statt 50;-)
- Preisschwellen durch Extras vertäglich d.h. rechtfertigbar machen
- zwei für eins (BOGOF, z.B. Zeitstunden)
- Rate decoy (s.o. versteckte Preissteigerung, Lockpreis)
- Produktverpackung aufmotzen (pimping, schminken, Mogelpackungen)
- Großpackungen
- Flat rate (all you can fuck)
- Abos (10 Besuche jetzt zahlen, 11ter gratis)
- Rabattmarken (payback)
- Membership (Kundenbindung)
- Affiliate Programme (Strukturvertrieb, aber Arbeitsteiltung in Prostitution verboten)
- Kobern / engl.: milking (Extras verkaufen)
- Angebotsaktionen (bei flauen Angebotszeiten)
- Visitenkarte als Werbegutschein (Networking)
- Werbung (Marketing) allgemein
- ...


Während der Käufer gerne emotional sein darf, zumal es bei Konsum und Sexdienstleistungen um emotionales Vergnügen und Ekstase geht, darf das dem Verkäufer langfristig oder schleichend möglichst nicht passieren. Das bedeutet einen extremen Spagat für alleinselbständige Sexworker mit Selbstverwirklichungsmotiv (SWBO-Gefahr). Der Sexworker ist sein eigenes Produkt. Das ist Problem und extreme Herausforderung. Sie wird mit dem Prostitutionstabu bestraft.

Allein deshalb ist Vorkasse im Sexbiz eine wichtige Psychohygiene, um Preisverhandlungs-Phase (Verkaufen) von Sexdienstleistungs-Phase (Liefern) sauber trennen zu können. Dass es sogar schon im alten Testament beschrieben ist hat mich selbst überrascht (Geschichte von SW Tamar).


Preisnachfragen insb. solche von Preisdumpern darf man/frau nicht an das persönliche Selbstwertungs-System heranlassen. Evt. helfen Auszeit, veränderte feste Arbeitszeiten, gute Freunde/Familie oder das nervig-anspruchsvolle Telefonanruf-Terminvereinbarungs-Geschäft von einer Telefonistin und Empfangsdame erledigen zu lassen (out-sourcen an vertrauenswürdige und gleichzeitig kompetente Kollegin/Freundin, indisches Callcenter oder 400euro-Jober_in. Denn allgemein gilt: Verkaufen d.h. Telefonieren ist Chefsache).


Weil jeder Arbeitsmarkt also auch unser Dienstleistungsmarkt für Sexdienstleistungen ein unperfekter Markt ist, gibt es bei niedrigen sinkenden Preisen Marktversagen! Wenn die Preise und der Umsatz nicht mehr zum Leben reichen, versuchen die Anbieter durch Preissenkung die Kunden zu halten und zu locken und gleichzeitig mehr zu arbeiten (runinöser Wettbewerb). Diese selbstverstärkende Selbstausbeutung und "-versklavung" kann langfristig nicht gut gehen. Dieses Eherne Lohngesetz hat schon Ferdinand Lassalle (1825-1864) erkannt:

• "Der Lohn schwankt bei vollkommener Konkurrenz unter den Bedingungen eines schrankenlosen Kapitalismus stets um das Existenzminimum".

Dr. Florian Bauer ist psychologischer Preisforscher (und Vorstand Vocatus AG) und hat weitere Tipps und Branchenbeispiele:
www.3sat.de/page/?source=/nano/gesellsc ... index.html
www.vocatus.de/publikationen/vocatus-artikel.php


http://de.wikipedia.org/wiki/Kategorie: ... %B6rderung
http://de.wikipedia.org/wiki/Kategorie:Marketing
http://en.wikipedia.org/wiki/Category:Sales_promotion





.

[Marc of Frankfurt]

"Zwangsprostitution" herrscht bereits auf dem allgemeinen Arbeitsmarkt
wg. staatlicher Sanktionspraxis von Arbeislosenversicherung und Jobcenter.
Erst versagte der Arbeitsmarkt (Marktversagen), dann das staatliche Sozialsystem:

Hartz IV wirkt nicht!
Die durchschnittliche Verweildauer in der Arbeitslosigkeit hat sich durch die Reform NICHT (weiter) verkürzt, sondern war vorher schon kurz (12 Monate für 50% der Arbeitslosen).


In zwei Kleinen Anfragen wollte die Linksfraktion von der Bundesregierung wissen, wie es um Arbeitsmarktpolitik und Grundsicherung bestellt ist.
Die nun vorliegenden Antworten zeigen die gewaltigen Defizite:

1:12 (uneschönt) oder 1:9 (geschönte Statistik) ist das Verhältnis von offenen Stellen zu Arbeitssuchenden, welches seit Jahren gilt.

Hartz IV Reform 2005 unter Kanzler Schröder (SPD) war die Umstellung von Sozial- und Arbeitslosenhilfe auf ALG II.

Beträge pro Monat:
935 Euro Armutsrisikogrenze im Jahre 2008.
746 Euro Arbeitslosengeld (ALG I gemäß SGB III) durchschnittlich gezahlt.
635 Euro Grundsicherung Hartz-IV (ALG II gemäß SGB II). D.h. 300 Euro unter Risikogrenze!
Daneben Wohngeld.

Massenhaft rechtswidrige Sanktionspraxis durch Verwaltungshandeln bei:
- ALG I (eine reine Versicherungsleistung)
ALG I verhindert nicht Einkommensarmut und damit verbundene Ausgrenzung von der gesellschaftlichen Teilhabe!
765.000 mal wurden Sperrzeiten verhängt, d.h.
66...75% aller Arbeitslosen wurden wg. angeblichem Fehlverhalten mit Leistungsentzug bestraft. Das heißt:
Kalte Enteignung von Versicherungsansprüchen/Ausgrenzung aus dem Leistungsbezug.
65% davon verhängt wegen »verspäteter Arbeitssuchendmeldung« oder einfach »Meldeversäumnis«.
10% aller Sperrzeiten wegen »Arbeitsablehnung« oder »Abbruch der Eingliederungsmaßnahmen« verhängt.

- ALG II (Harz-IV)
Hartz IV schützt nicht vor Einkommensarmut und damit verbundener Ausgrenzung von der Teilhabe an der Gesellschaft!
67% der offiziell als arbeitslos Registrierten sind im Hartz-IV-Bezug.
16% (jeder sechste) wurden sanktioniert (Leistungskürzungen)
Die sanktionsbewehrte "Aktivierung" (Meldepflichten, Eingliederungsvereinbarungen und -maßnahmen...) läuft auf Hochtouren, obwohl tatsächlich nur sehr wenige Erwerbsarbeitsstellen zu vermitteln sind.
Hartz IV ist Armut und Ausgrenzung durch Sanktionen!
7.000 Klagen gab es weil gar nichts mehr gezahlt wurde.
60% davon waren erfolgreich.

Erfolgsquote bei Prozessen gegen falsche Bescheide:
40% bei ALG I - 17 Monate durchschnittliche Dauer erstinstanzliches Klageverfahren
33% bei ALG II - 11 Monate

Verdeckte Armut:
Die Quote der verdeckten Armut im SGB II und SGB XII liegt bei rund 50% d.h. auf einen Transferbeziehenden kommt noch ein Anspruchsberechtigter in verdeckter Armut.
Oder anders: Mit den Grundsicherungssystemen werden ca. 50% der Anspruchsberechtigten aus der ihnen zustehenden Absicherung des ohnehin schon zu niedrigen Existenz- und Teilhabeminimums ausgrenzt.

FAZIT: Derzeitige Arbeitslosenversicherung bedeutet:
- Armut und Ausgrenzung per Gesetz (durch zu niedrige Leistungen) und
- massenhafte Ausgrenzungen aus dem Leistungsbezug (durch rechtswidriges Verwaltungshandeln, durch Sanktionen/Sperrzeiten und durch verdeckte Armut)!

Wer sich (rechtlich) wehrt, lebt nicht verkehrt!





Sozialpolitischen Sprecherin der Linksfraktion, Katja Kipping:
"Auswertung Kleine Anfragen Arbeitsmarkt und Grundsicherung Hartz IV"
www.katja-kipping.de/serveDocument.php? ... f/1a77.pdf
www.katja-kipping.de/article/459.wenige ... ionen.html
www.neues-deutschland.de/artikel/199127.html

Antworten der Bundesregierung
http://dipbt.bundestag.de/dip21/btd/17/055/1705583.pdf Arbeitsmarktpolitik und damit verbundene soziale Aspekte
http://dipbt.bundestag.de/dip21/btd/17/058/1705861.pdf Grundsicherung und damit verbundene soziale Aspekte)

Protokolle, Videos und weitere Materialien zur ersten Lesung und zur öffentlichen Anhörung im Bundestag
www.katja-kipping.de/article/475.wortpr ... ungen.html

"Abschaffung der Sanktionen!", Stellungnahme von Prof. Dr. Stephan Lessenich (Uni Jena)
www.youtube.com/watch?v=382_uz043ms
www.katja-kipping.de/article/470.sankti ... neben.html

Theorem der Arbeitslosigkeitsfalle, welches auch Begründung der Hartz-IV-Gesetzgebung war (Hartz-IV-Aktivierungsideologie) beruht offensichtlich auf einer falschen Annahme (existierte gar nicht). Die Reform hatte keinen Nutzen!
Mögliche negative Folgen der Hartz VI Reform sind:
- eine Zunahme von sozialer Ungleichheit und Armut,
- höhere Beschäftigungsunsicherheit sowie
- Armut trotz Arbeit (working poor), das sind
- soziale Reformkosten die zu Buche schlagen und
- verletzte Gerechtigkeitsnormen.
Studie von Georg Vobruba (Universität Leipzig) und Sonja Fehr (Institut für Arbeitsmarkt und Berufsforschung)
www.boeckler.de/pdf/pm_wsi_2011_05_30.pdf


http://de.wikipedia.org/wiki/Arbeitslos ... schland%29
http://de.wikipedia.org/wiki/Arbeitslosengeld_II
http://de.wikipedia.org/wiki/Arbeitslosenstatistik
...

Das hat zwar alles mit Sexarbeit nicht dirket zu tun, ist aber so unsexy, dass es viele in die Sexarbeit "treibt", dort unter besseren äußeren Bedingungen (nicht verwechseln mit Arbeitsbedingungen Sexwork) ihr Glück und Auskommen zu suchen.





.

[Marc of Frankfurt]

Berlin (ots) - Presseerklärung Bundesverband der Deutschen Volksbanken und Raiffeisenbanken (BVR):


Umfrage: Deutsche verfehlen ihr Sparziel um 30%

Die Bundesbürger sparen nach eigener Einschätzung nicht genug.


Sie legen zwar jeden Monat durchschnittlich 180 Euro auf die hohe Kante.

Zur Erfüllung ihrer Ziele bräuchten die Bundesbürger jedoch nach eigener Meinung im Durchschnitt 250 Euro jeden Monat.

Sie sparen also statt wie exakt ermittelt 256 Euro - 180 Euro, also monatlich 76 Euro beziehungsweise 30% zu wenig.

Dies ist das Ergebnis einer aktuellen Umfrage von TNS-Infratest im Auftrag des Bundesverbandes der Deutschen Volksbanken und Raiffeisenbanken zum Sparverhalten der Deutschen.

Befragt wurde eine für Deutschland repräsentative Auswahl von 2.075 Bundesbürgern im Frühjahr 2011.

"Zwischen Vorsorgebedarf und Spartätigkeit zeigt sich eine Lücke. Viele Bundesbürger sehen ihre finanziellen Möglichkeiten als nicht ausreichend an, um ihre Sparvorhaben vollständig zu verwirklichen. Die gute Arbeitsmarktentwicklung wird aber helfen, die Sparlücke zu verringern. In diesem und im kommenden Jahr dürften die Einkommen der Bundesbürger auch preisbereinigt zunehmen", erläutert BVR-Vorstandsmitglied Dr. Andreas Martin.

Nicht alle Bevölkerungsgruppen verfehlten der Umfrage zufolge ihr Sparziel in gleicher Weise: Junge Bundesbürger und Geringverdiener hätten bei der Erreichung ihrer Sparziele die größten Probleme. Hier gingen Sparziel und tatsächliches Sparen zum Teil am deutlichsten auseinander.

Demgegenüber falle die Sparlücke bei den Beziehern höherer Einkommen und bei älteren Befragten niedriger aus.

Trotz der starken gesamtwirtschaftlichen Schwankungen im Zuge der schweren Rezession 2008/2009 und der anschließenden raschen Erholung der deutschen Wirtschaft blieb die Sparquote der Bundesbürger vergleichsweise stabil.

Im Jahr 2010 haben die Sparanstrengungen nach Angaben des Statistischen Bundesamtes etwas zugenommen.

Die Sparquote der Bundesbürger, das heißt das Verhältnis des Sparens zum verfügbaren Einkommen, stieg um 0,3 Prozentpunkte auf 11,4 Prozent.

D.h. die Leute legen 11,4% vom verfügbaren Einkommen zurück !!!

"Die gefestigte konjunkturelle Dynamik in Deutschland und die verbesserten Einkommensperspektiven lassen die Konsumneigung der Bundesbürger nun wieder geringfügig ansteigen. Wir erwarten daher für das Jahr 2011 einen leichten Rückgang der Sparquote um 0,2 Prozentpunkte auf 11,2 Prozent", so Martin.

Die von den privaten Haushalten für die Geldvermögensbildung verwendeten Mittel stiegen in 2010 um 6,7 Milliarden Euro auf 153,6 Milliarden Euro.

Dabei blieben Einlagen bei Banken die beliebteste Anlageform der Deutschen. Insgesamt 80,3 Milliarden Euro flossen den Bankhäusern in Deutschland zu. Versicherungen zogen im gleichen Zeitraum 63,1 Milliarden Euro auf sich, Wertpapiere lediglich 0,2 Milliarden Euro.

Der Bestand an Geldvermögen erreichte Ende 2010 mit 4.934 Milliarden Euro fast die 5-Billionen-Marke.

[Vgl. Schuldenstand der Öffentlichen Haushalte von Städten, Ländern und Bund (D): 2 Billionen Euro.]

Im Durchschnitt verfügte jeder Haushalt in Deutschland über ein Geldvermögen in Höhe von 122.700 Euro, dem Verbindlichkeiten von 38.200 Euro [31%] gegenüberstanden.

Das ergibt ein Netto-Geldvermögen von 84.500 Euro pro Haushalt.

Die aktuelle Studie des BVR ist im Internet unter www.bvr.de , Publikationen, Konjunkturberichte abrufbar:
www.bvr.de/p.nsf/995D9E5CC02254EAC12578 ... ialNr9.pdf

Originaltext: BVR Bundesverband der dt. Volksbanken und Raiffeisenbanken Digitale Pressemappe: www.presseportal.de/pm/40550 - Pressemappe via RSS: www.presseportal.de/rss/pm_40550.rss2

Pressekontakt: Bundesverband der Deutschen Volksbanken und Raiffeisenbanken - BVR Pressesprecherin: Melanie Schmergal Schellingstraße 4 10785 Berlin Telefon: (030) 20 21-13 00 Telefax: (030) 20 21-19 05 Internet: www.bvr.de E-Mail: presse ät bvr.de





Ferner muß man berücksichtigen, dass hier höchstwahrscheinlich mehrheitlich Angestellte und Arbeiter befragt wurden, für die sich zusätzlich und quasi automatisch eine Rente anspart.

Alleinselbständige Sexworker müssen also insgesamt noch mehr jeden Monat zurücklegen (einmal in Höhe der Rate für die Sozialversicherungen (Minimalrente) plus eine Spar-Rate = 350 + 250 = 600 Euro pro Monat).

Eine wichtige Kennzahl, die jeder Sexworker bei einer Einstiegsberatung erfahren sollte! Bisher habe ich etwas vergleichbares im Umfeld der 'Hurenberatungsstellenbewegung' noch nie gehört.





.

[Marc of Frankfurt]

Immer noch Ungereimtheiten bei der Aufarbeitung der Finanzkrise seit 2007:


Entgegen jeder Vernunft behaupten die Ökonomen noch immer, Wachstum würde Schulden tilgen.

Schulden sind eine Fixgröße (Zeitpunkt),
Bruttoinlandsprodukt (BIP, vgl. Umsatz, Gewinn) sind Fließgrößen (Zeitperiode).

In keiner Unternehmensbilanz [oder Einnahmen Überschuß Rechnung] ist es gestattet, Schulden gegen Umsätze zu rechnen!

Und das ganze wird von nur 3 US Ratingagenturen bewertet, die von den beauftragenden Unternehmen selbst bezahlt werden...

[ Für mich ein globales System wegdelegierter Verantwortung, unkontrolliert geschaffenen hemmungslosen Profitmöglichkeiten, Ausbeutungsverhältnisse und Abhängigkeiten durch Zinsknechtschaft wie in betrügerischen Bordellen (Blockschulden). ]


Ob ein Überang vom manipulierbaren übermächtigen Finanzkapital zu humanem Sozialkapital gelingt, damit die Menschen wieder dem System vertrauen?

Vertrauen aber ist eine der wichtigsten Grundlagen des sogenannten Sozialkapitals. Als Sozialkapital können die nichtmateriellen Dinge bezeichnet werden, die eine Gemeinschaft verbinden. Neben Vertrauen sind das Geschenke, Hilfsbereitschaft, Solidarität und Gastfreundschaft.

Wertewandel und Rating-Revolution wird im Grassroot-Bereich stattfinden müssen.

[ Sozialkapital muß sich nach Revolution oder Krise ganz neu aufbauen, so wie nach einem Krieg oder Konkurs materiell-finanziell ganz neu angefangen werden muß. ]


http://derstandard.at/1310511434146/Soz ... r-Waehrung





Da die meisten Sexworker ein Doppelleben führen als Schutz gegen mögliche Stigmatisierungen, kann sich bei ihnen nur sehr eingeschränkt Sozialkapital aufbauen. Während z.B. ein Lebensberater oder Buchautor mit jedem Kundenkontakt, Veranstaltung oder Veröffentlichung seinen immateriellen Marktwert (Sozialkapital) erhöht kann das bei Sexworkern das genaue Gegenteil bewirken, diskretionsbedürftige wohlhabende Kunden bleiben fern und eine soziale Gefahr kann entstehen für das Privatleben und die Familie.

Diesen immateriellen Wertverzicht bzw. akkumulierten Verlust über die Jahre in der Sexarbeit hat noch nie jemand versucht richtig auszurechnen und zu bewerten. Ich vermute hier liegt ein wichtiger versteckter ökonomischer Grund für das langfristige Scheitern vieler Sexworker.

Es gelingt ferner den wenigsten Sexworkern den sich erarbeiteten Ruhm in der Sexarbeit auf spätere berufliche Aktivitäten zu übertragen (Gina Wild > Michaela Schaffrath). Daneben ist eine Gewinn-/Verlustübertragung von Sexwork zum Ex-Sexwork-Betrieb steuerrechtlich verboten!

Hinzu kommt, dass Sexworker ihre Produktionsanlagen ("Mein Körper ist mein Kapital") nicht abschreiben und steuerlich absetzen dürfen. Das wär ja noch schöner. *lach*





.

[Marc of Frankfurt]

Die Geschichte des Geldes ist gar nicht sexy sondern blutig!


Weisheit über Geld und Macht im Märchen:

Der Zauberer von Oz



US-Kinderbuch 1900
von Lyman Frank Baum

Verfilmt mit Judy Garland 1939.


Hier der sehr erhellende Dokumentarfilm: "Das Geheimnis von Oz"
vom Journalist Bill Still 2009
(110 min):
www.youtube.com/watch?v=RKMpjrw2Sm0 Deutsch synchronisiert
www.youtube.com/watch?v=7qIhDdST27g Englisch original

Es geht um die Finanzkrise heute wie damals, um die Fehler im Geldsystem und wie eine Finanzoligarchie der Bankster stets versucht die Kontrolle zu erlangen mit knappem verzinstem Schuldgeld... Eine Geldgeschichte seit Jesus, der die Händler aus dem Tempel wirft, bis zur heutigen Bankenrettung (to big to fail). Derzeit nicht anders als um 1900. Der Film zeigt wie der Autor sein Wissen über die Geldgeschichte und seine politische Kritik im Märchen verschlüsselt hat.

[youtube]http://www.youtube.com/watch?v=RKMpjrw2Sm0[/youtube] www.secretofoz.com
www.theMoneymasters.com/mm/
http://en.wikipedia.org/wiki/The_Money_Masters
Sein neues Buch "No more national debt":
www.kickstarter.com/projects/billstill/ ... ional-debt
- no national money borrowing = plutocracy
(sovereignty = self issued money + independently controlled money base)
- no fractional reserve banking = lending money private banks don't have
(lending leverage 1:10...12, in 2008 1:52, up to Goldman Sachs 1:333)
www.youtube.com/user/bstill3





Im Film kommt auch das erfolgreiche englische Geldsystem der Tallysticks (Kerbhölzer) vor. Dem entspricht das uralte Chinesische System Fei Lun (fliegendes Rad):
www.sexworker.at/phpBB2/viewtopic.php?p=106183#106183





Literatur:
Stephen Zarlenga:
Der Mythos vom Geld - die Geschichte der Macht
2. Aufl. 2008:
www.amazon.de/dp/303509005X

Vergleichbares auch in Goethes "Faust II" von 1821
vom Schweizer Nationalökonom Prof. Hans Christian Binswanger: "Geld und Magie - ökonomische Interpretation von Goethes Faust"
3. Aufl. 2009:
www.amazon.de/dp/3938017252

[Marc of Frankfurt]

So kalkuliert ein alleinselbstständiger Dienstleister oder Sexworker den Preis für seine Dienstleistung:


www.muenster-gruendet.de/media/checklis ... istung.pdf
(2 Seiten, 6 KB)





http://en.wikipedia.org/wiki/Cost-plus_pricing

[Marc of Frankfurt]

Ökonomie der Sexarbeit:

Geld-Theorie und SW-Lebenslaufbetrachtung


Selbstversorgung / Fremdversorgung
Zuerst unterscheidet man Selbstversorgungswirtschaft (traditionelle Bauerngesellschaft) und Fremdversorgungswirtschaft (moderne Industrie- und Dienstleistungsgesellschaft). In der Selbstversorgungswirtschaft kann man auch ohne Geld und Tausch überleben nur von dem was der eigene Boden (oder Gemeinschaftswald, Allmende) hergibt. In der modernen Gesellschaft in den Städten geht ohne Geld (und Kredit) gar nichts. Im Sexuellen kann die Ehe als Selbstversorungswirtschaft verstanden werden, während Sexwork-Paysex der Fremdversorgungswirtschaft entspricht.

Economic Theory of Prostitution

Warengeld / Informationsgeld
Darüberhinaus gibt es eine möglicherweise noch viel wichtigere Unterscheidung, die zwei verfeindeten ökonomischen Schulen entspricht:
- Die Anhänger der Lehre der Tauschwirtschaft (Geld ist Tauschmittel)
- und diejenigen, die die Geldentstehung aus Schuldquittungen (Kredit, Quittungsschein) erklären (Geld ist Verschuldung, jedem Guthaben entspricht ein Kredit, eine Schuld), der Kreditwirtschaft = Schuldgeldwirtschaft = Debitismus (Prof. Dr. Otto Steiger (R.I.P.), Prof. Gunnar Heinsohn, Dr. Paul C. Martin, Prof. H.C.Binswanger).

Die meisten Leute wissen gar nichts über diesen grundsätzlichen Unterschied oder Wissenschaftsstreit und die Tauschwirtschafts-Lehre ist unhinterfragt die offizielle Theorie und herrschende Politik. Möglicherweise aber alles Propaganda bzw. Vernebelung (Geldschleier der Finanzoligarchie).


Dabei muß bei Geldentstehung unterschieden werden zwischen dem historischen Prozess und der heutigen Praxis:

Erste Geldmünzen gab es z.B. 700 v.Chr. in Lydien (Goldmünzen von König Krösus, heutige Türkei, im Bild links, Vollgeld, Selbstwertgeld, weil der Geldwert vom Sachwert des Materials gedeckt ist). Noch älter sind aber Kreditgeld-Scheine z.B. als Tonscherben-Getreidelager-Quittungen z.B. in Ägypten (angedeutet mit dem Bild rechts, griech.: Ostraka, Kreditgeld, Schuldgeld, Fiat-Money, weil der Geldwert durch Vertrag und Konventionen i.V.m. staatlichen Gesetzen und Gewaltmonopol garantiert ist). Auf der Tonscherbe steht sinngemäß wie auf modernen Geldscheinen: "Gegen Einlösung dieser Urkunde wird soundsoviel (Getreide/Gold...) ausgezahlt" (staatlich garantiertes Annahme-Zwangs-Geld). Statt mit dem Getreide oder Gold selbst zu tauschen war es irgendwann einfach praktischer und sicherer diese Quittungen zum Einkaufen zu tauschen.

Ähnlich verläuft die heutige tägliche Entstehung von Geld und Kredit (durch sogenannte Geldschöpfung von Fiat-Money, fiat lat.: erzeugt, gemacht) auf folgenden vier Wegen in unserem zweistufigen Bankensystem: (I.) durch Bundesbank/Eurozentralbank (EZB): (1) Zentralbankgeld (=Geldscheine) und (2) Quantitative Easing/Offenmarktpolitik d.h. Ankauf von (Staats)anleihen (Zentralbank-Buchgeld d.h. Geldkreislauf nur für Staaten und private Banken bei der Zentralbank) ... und (II.) durch die privaten Geschäftsbanken: (3) Buchgeld =Giralgeld =Bankguthaben =Kredit =Schuldgeld und (4) Fractional Reserve Banking (Mindestreserve, d.h. die Bank braucht nur den Bruchteil von 2 bis 8% Eigenkapital-Reserve zu haben für 100% Kredit den sie verleiht und an dem sie voll Zinsen verdient. Diese Money-Multiplier-Mechanik hat sich inzwischen als mythischer Nebel erwiesen. Es ist lediglich eine rechtliche Vorgabe, die in der Praxis fast nicht relevant ist, weil die Banken zunächst unbegrenzt schöpfen können und erst später schauen, wie sie die gesetzlichen Vorgaben erfüllen. Ferner können Banken, wenn der Kreditnehmer säumig wird, d.h. mit nur wenigen Rückzahlung in Verzug gerät, vom Schuldner das komplette Pfand verlangen, egal wie viel schon getilgt wurde: Forderungsweiterverkauf, -Verbriefung, Inkasso: Pfändung und Zwangsversteigerung. Der Geldverleiher, die Bank gewinnt immer (legale Enteignung). Und die Schuld wird wie das Wort schon sagt allein dem Schuldner angelastet, während der Gläubiger, der sich verspekuliert hat geschützt wird (Opfer-Schuld-Umkehr). Allein schon unser heutiges Bargeld aus Münzen und Scheinen entstammt aus beiden entgegengesetzten Traditionslinien, Tauschgeld und Kreditgeld oder Warengeld und Informationsgeld, denn das Papiergeld kann als ein verteiltes Buchhaltungssystem auf Zetteln verstanden werden:

Goldklumpen genauso wertvoll wie Tonscherbe?!
Älteste Münze und Geldschein (Zertifikat): Selbstwertgeld (li.) und Schuldvertragsgeld (re.)
Warengeld versus Informationsgeld.

Tatsächlich hat Geld natürlich beide Funktionen (1) Tausch und (2) Kredit, wobei Kredit die viel ältere ist. Nebenbei bemerkt gibt noch weitere Geld-Funktionen: (3) Signalfunktion Preisbildung (Wertmitteilung, Kommunikation, Vergleichsmaßstab) und (4) Horten (Sparen, Wertaufbewahrung, Zukunftsvorsorge; vgl. Thesaurierung, Geldwertproblem) und (5) Steuerschuld-Tilgungsmittel (Diese dem Buch- oder Papiergeld letztlich seinen Wert verleihende Funktion, begründet auch warum der Staat bei jeder Form des Geldverdienen also auch beim Sex-gegen-Geld-Tasch Steuern beansprucht für sein staatlich kontrolliertes und gesichertes Geld). Heute muß man sich aber fragen, was ist der bedeutsamere und entscheidende Mechanismus des Geldes und der Geldentstehung bezogen auf die tatsächliche oder täglich entstehende Geldmenge, Kreditvergabe und Verschuldung z.B. von ganzen Staaten. Inflation, Konkurs, Finanzkrise und Staatsbankrott zeigen, dass mit einem Schlag riesige Geldmengen vernichtet werden können, ohne dass Waren oder Arbeitskraft zerstört worden wären (also ist nur Buchgeld bei platzenden Finanzblasen =Crashs betroffen: Geldmengen M1 bis M3). Aber die eigentlichen Werte sind nunmal die Güter und nicht das Papier-Geld ("Geld und auch Gold kann man nicht essen"). Das meiste Geld sind ferner nicht Münzen und Scheine (Teil der Geldmenge M1) sondern Giralgeld auf Konten (Büchern) und Eigentumsverträge (Schuldverschreibungen, Geldmarktpapiere...). Während M1 die Geldmenge des kleinen Mannes ist (Konsument) ist M3 die viel größere Geldmenge der Investoren und Kapitalisten. Bundesbank und EZB messen, beeinflussen und veröffentlichen diese Geldmengen regelmäßig (Geldpolitik).
http://de.wikipedia.org/wiki/Geldmenge





Tauschen / Wirtschaften
Der Unterschied zwischen Handel als reiner Tausch und Handel auf Kredit ist die Zeit. Tauschhandel braucht nur die Gegenwart oder Gleichzeitigkeit. Das entspricht einem Leben im hier und jetzt (paradisisch, tierischer Naturzustand) und ist damit das Gegenteil von dem was die meisten Leute tun müssen, nämlich fleißig lernen und hart arbeiten für einen vielfach nur geringen Lohn und Rente.

Handel auf Kredit hat immer zwei Zeitpunkte und eine dazwischenliegende unsichere Phase (1. Verschulden =Vorfinanzieren =Investieren =Versprechen und Risiko eingehen und 2. Abbezahlen, Rückzahlen =Kasse machen =Rendite, Gewinn Mitnahme =Rekapitalisierung, Bilanz glattziehen).
Während der simple Handel ein nur "Tauschen" ist, kann erst die zweite Variante mit Berücksichtigung der Zeit als "Wirtschaften" benannt werden. Es muß nicht nur die Unsicherheit des Fremden (Geschäftspartners) und des Produktes als Risiko ausgehalten werden (Betrugsgefahr), sondern auch die größere fundamentale Unsicherheit und Offenheit der Zeit und Zukunft.

Allein dadurch, dass Herstellung von Waren Geld kostet, genauso wie Ausbildung der Dienstleister_innen (Schulgeld) und finanziert werden muß bevor Geld verdient werden kann, existiert und ist Kredit notwendig. Die Notwendigkeit von Vorfinanzierung und das damit immer verbundene Wagnis ist der Kern allen Wirtschaftens und Investments = guter Kredit (im Gegensatz zu schlechtem Kredit für Konsum oder Umschuldung oder zur Bezahlung von Schuldenraten, was in die Schuldenfalle führt).

Wert der Arbeitsfähigkeit / Wert der Arbeitsprodukte
Insbesondere müssen die Kosten und Lebenshaltungskosten in der Zwischenzeit vor-finanziert werden (Zeit ist Geld). Weil die meisten Menschen das nicht können/wollen, können sie auch nicht selbstständig werden, sondern müssen abhängig Beschäftigte bleiben (Lohnsklaven) und müssen ihre Arbeitsfähigkeit oder Arbeitskraft komplett verkaufen (beim Einstellungsvertrag und allen weiteren Stufen während sie an der Karriere basteln). Ein Selbständiger hingegen verkauft den Wert seiner Produkte oder Arbeitsergebnisse. Der Wert der Arbeitsprodukte (Output) ist höher als der Wert der Arbeitskraft (Input). Die Differenz ist der Mehrwehrt und das ist sein Unternehmerlohn.

Tauschwert / Gebrauchswert
Damit verkauft der Arbeiter auf dem Arbeitsmarkt nicht nur den Tauschwert (Marktwert) seiner erbrachten Arbeitsleistung, sondern auch den Gebrauswert seiner Arbeitskraft für den Unternehmer. Den Mehrwert (Unternehmerlohn) seiner Arbeitskraft bekommt der Boss oder bei der Sexarbeit der Betreiber. Dieses ökonomische Grundprinzip bei Arbeitsteilung und ohne jegliche Betrachtung sonstiger Zwangs- oder Gewaltanwendung hat Karl Marx als Ausbeutung (Mehrwertbeschneidung) bezeichnet. Achtung: es wird in der Ökonomie völlig anders verwendet als der strafrechtliche(!) Begriff Ausbeutung im Zusammenhang mit Prostitution!). Die Mehrwertbeschneidung ist der Unterschied zwischen dem was der Kunde bezahlt und was der Arbeiter bekommt. Z.B. bekommmt ein Sexworker im Bordell meist 50% oder ein Web-Cam-Sexworker oftmals nur 40-20% von den 100% Tauschwert, die ein alleinselbstständiger Sexworker bekommt und ein Kunde bezahlt, wenn er sich einen gleichgroßen oder größeren Nutzwert (Gebrauchswert) verspricht (zufriedener Kunde).

Letztlich ist es der Zeitfaktor oder die Angst in Zukunft ohne Einkommen und Arbeit zu verhungern oder sozial abzusteigen, der die Menschen zu Lohnsklaven macht und zu Lohn- und Preisdumping auf dem Arbeitsmarkt führt. Es trifft auch für den Markt der Sexdienstleistungen zu, weil dieser gleichzeitig sowohl ein Dienstleistungsmarkt für den Kunden als auch ein Arbeitsmarkt für den Sexworker ist. Das für Arbeitsmärkte typische Marktversagen kann auftreten d.h. Mehrarbeit trotz Preisverfall: immer mehr arbeiten müssen für immer weniger Geld (Ehernes Lohngesetz von Ferdinand Lassalle 1825-1864).





Der Zeitfaktor ist aber ganz entscheidend bei Wertschöpfung und Produktion (Wachstum, Herstellung, menschliche Arbeit, Güterentstehung). Nur wenige Händler (Broker), Tagelöhner oder Sexworker brauchen keine Wertschöpfungszeit zu berücksichtigen, sondern nur zu tauschen. Sie vernachlässigen die Reproduktionskosten der Arbeitskraft und können insofern 'von der Hand in den Mund leben'. Alle anderen müssen erst planen-investieren, sähen-ernten, transportieren-lagern, arbeiten-produzieren und den Zeitfaktor und Vorfinanzierung berücksichtigen bevor sie tauschen können. Dafür müssen und dürfen sie die verbrauchte Zeit d.h. Kosten der Herstellung und Reproduktion (Herstellung und Erneuerung der Herstellungsmittel) später abschreiben. Abschreiben heißt die angelaufenen Kosten inklusive Verschuldung d.h. Kreditkosten (Kapitalmarktkosten, Zinsen) in kleinen Einheiten auf den Preis umzulegen oder von der Steuer abzusetzen. Heute ist ferner die meiste Wertschöpfung arbeitsteilig organisiert. Man kann sagen Arbeit ist heute sowohl in der Zeit als auch im Raum (Orts- und Phasenraum) ausdifferenziert. Beides, Abschreibung und Arbeitsteiligkeit ist Sexworkern verboten! Wir dürfen den Zeitwert unserer Produktionsanlagen weder steuerlich abschreiben, noch dürfen wir vollumfänglich arbeitsteilig arbeiten, wenn wir nicht wegen Zuhälterei und Menschenhandel angeklagt werden wollen. Sexwork wird wie Sexualität dem Konzept und der Sphäre der Natürlichkeit und Privatheit untergeordnet und damit kulturell abgegrenzt gegenüber den meisten Arbeits- und Wirtschaftsformen der Sphäre Kultur und Öffentlichkeit (Fundamentalistisch-religiöser Dualismus von Natur-Kultur, Materie-Geist, Böse-Gut). Deshalb wird Sexwork systematisch benachteiligt (Exklusion). Dies geschieht bekanntlich und vorgeblich um Sexworker vor Mißbrauch wie Zuhälterei und Menschenhandel zu schützen, aber bedeutet gleichzeitig eine strukturelle Sonderbehandlung (Paternalisierung d.h. Sexworker werden wie Kinder gegängelt), die ihren wirtschaftlichen Erfolg behindert und abschneidet (Prostitutionseindämmung bewirkt Präkarisierung).





Die Lehrsätze zum Tauschhandel der herrschenden Lehrmeinungen Klassik und Neoklassik sind nur sehr eingeschränkt richtig (Dogmen, Mythen). Manche sagen sie gehören auf den Müll.

- Saysches Theorem von 1803
Jedes Angebot schafft sich seine Nachfrage selbst.
(Es gibt kein Marktversagen)
http://de.wikipedia.org/wiki/Saysches_Theorem

- Neutralität des Geldes von 1896
Nach klassischen und neoklassischen Vorstellungen besteht eine Dichotomie (griech. Zweiteilung) zwischen dem realen und monetären Sektor der Volkswirtschaft. Störungen, die im monetären Sektor auftreten, übertragen sich nicht auf den realwirtschaftlichen Bereich. D.h., Durch Geldmenge werden nur nominale Größen wie Preisniveau beeinflusst, aber nicht reale Größen wie Produktionsniveau...
(Geldnebel, Schleier des Geldes)
http://de.wikipedia.org/wiki/Neutralit% ... des_Geldes

- Homo Economicus
- Unsichtbare Hand
Homo Economicus heißt egoistische Wirtschafts-Subjekte, wo jeder gegen jeden kämpft auf dem Markt. Dann aber soll dank irgendwie göttlicher Einwirkung ein Marktgleichgewicht und ein Bruttosozialprodukt zum Wohle aller herauskommen.
(Adam Smith war Theologe)





Der Sexworker befindet sich unsprünglich und dem Prinzip nach im Status der Tauschwirtschaft, weil er scheinbar unbegrenzt die Ressource Sexdienstleistung abrufen und verkaufen kann (Sexapeal, Jugend, Schönheit, Exotik, Trieb, Offenheit, Willigkeit, (Abenteuer)lust...). Weil dieses freie ökonomische Leben 'im hier und jetzt' den meisten Menschen verwehrt ist und sie stattdessen hart arbeiten müssen, erklärt sich aus diesem Gegensatz ein Großteil von Unwissen, Neid oder Haß gegenüber Sexworkern.

Wenn die Tauschmöglichkeit und damit Marktmacht des Sexworkers versiegt, nach einer Zeit in Freiheit wo sie wie sexuelle Millionäre leben konnten, z.B. wegen (SWBO, Alter, Unfall, Krankheit, Sucht, Gewalterlebnis, Gesetzeskonflikt...), dann verarmen viele Sexworker und werden zum Sozialhilfefall oder müssen sich in einem schmerzvollen Umstellungsprozess für den das Wort Ausstieg (Exit www.sexworker.at/exit Outplacement, Sexworker-Karriere) verwendet wird, eine abhängige Beschäftigung suchen bzw. zuvor umschulen oder ausbilden lassen. Die allgemeine Einführung von Ausbildung und Schulpflicht kann als sozialstaatliche Erfindung verstanden werden (vergleichbar der Einführung der Sozialversicherungssysteme), um das Leid der Arbeiter zu begrenzen, zu früh aus dem Arbeitsmarkt rausgeworfen zu werden, wenn sie körperlich nachlassen und unqualifiziert sind. Staatlich finanzierte Ausbildungszeit ist also eine Reaktion auf den mit der Industrialisierung verschärften Konflikt und Klassenunterschied zwischen Arbeit und Kapital, der letztlich auf dem Geheimnis basiert zwischen nur gegenwartsbezogenem Tauschen und vorausschauenden Wirtschaften von Vollgeld und Schuldgeld (Warengeld und Informationsgeld). Mit der Schulpflicht hat quasi der Staat anstelle der einzelnen Arbeiter wirtschaftlich vorausschauend gehandelt und zwingt seither alle zu ihrem Glück. Denn letztlich ist Schule eine Zwangsveranstaltung, wo jedoch im Gegensatz zu Prostitution so gut wie nie das Wort Zwang gebraucht wird, es sei denn der Schulschwänzer muß von der Polizei abgeholt werden. (Das Zwangsempfinden und gesellschaftliche Widersprüche werden auf Prostitution projiziert und dort stellvertretend abgestraft gemäß Sündenbockmechanismus [Cora Molloy, HWG Frankfurt].)

Da es weder Sexworker-Ausbildung noch geregelte Sexworker-Karrieren für eine Zeit nach der aktiven Sexarbeit gibt, wenn man kein Betreiber, Zuhälter oder Madam werden will (eine Management-Laufbahnen ist nicht vorgesehen, wegen Tabu der Arbeitsteiligkeit im Sexbiz), fallen die meisten Sexworker frühzeitig aus dem System und manche verarmen ("Hurengut paßt in einen Fingerhut"). Es sei denn sie haben selbst vorgesorgt (vorausschauend gewirtschaftet und den Zeitfaktor und Zukunft rechtzeitig bedacht und konnten Investieren in sich (Ausbildung, bürgerlicher Beruf) und Zukunftsvorsorge (Haus, Kapitalanlage). Sich fortgebildet bzw. gespart zu haben d.h. Qualifikationen (soziales Kapital) und monetäres Kapital akkumuliert zu haben). Dann können sie nach der aktiven Sexarbeitszeit investieren und umsteigen in ein anderes Geschäft (Nagelstudio, Café...). Das kann jedoch nur dann gelingen, wenn die hier erläuterte Theorie des Debitismus vom Schuld-Geld und zeitüberbrückenden Kredit verstanden wurde und sei es auch nur unbewußt.

gegenwartsbezogenen / zukunftsplanend
Ein erfolgreicher Sexworker/Ex-Sexworker, Unternehmer oder Kapitalist muß also das leisten, was die Gesellschaft als ganzes bisher noch nicht verstanden hat in Bezug auf Geldsystem und Wirtschaft. Um dieses Mehr leisten zu können, was über das reine gegenwartsbezogene Tauschen hinausgeht und fürs zukunftsvorsorgende Wirtschaften qualifiziert, braucht es gute Startbedingungen (Herkunft), starken Antrieb (Disziplin), Wissen (Sexworker Akademie, Sexworker Forum), viel Training (Versuch und Irrtum), Selbstsicherheit (Fehlertoleranz, Eingebundensein, Unterstützernetzwerk), Durchsetzungsvermögen (Ausdauer, Beharrlichkeit)... und natürlich auch eine große Portion Glück im Umgang mit den zahlreichen aufgestellten Fallen für Sexarbeiter und Unternehmer, nicht zu schweigen von den gläsernen Decken für Frauen und Prostituierte.

Einem erfolgreich ausgestiegenen Ex-Sexworker und weiterhin selbständigen Unternehmer muß also der Umstieg von einer 'naturnahen', aufs-heute-bezogenen Tauschwirtschaft zur arbeitsteilig, vorfinanzierten und zeitverrechnenden Kreditwirtschaft gelungen sein. Ein sehr anspruchsvoller Systemwechsel, der vmtl. nur entsprechenden Charakter-Typen gelingt.





Sexworker Outplacement, Ausstiegswissen, Huren-Karriere-Management (HKM):
www.sexworker.at/exit

Grundkurs monetäre Alphabetisierung von Jörg Buschbeck:
www.global-change-2009.com/blog/grundku ... n/2011/07/
www.youtube.com/watch?v=Lp_BvqcCGwA (Vortrag 1 Std.)

Geldformen und Schlepperei/Menschenhandel:
www.sexworker.at/phpBB2/viewtopic.php?p=107890#107890





.

[friederike]

@Marc,

das Steuer- und Sozialsystem ist, meine ich, für alle Berufe ungerecht, die keine konstante (oder sogar ansteigende) Einkommensentwicklung erwarten lassen: Sportler, Artisten, Künstler und natürlich auch SexarbeiterInnen. Das jeweils jährliche Einkommen wird voll versteuert, unterliegt der Progression (die deshalb sehr ungerecht ist, obgleich Politiker immer genau eine scharfe Progression als gerecht darstellen), während bei betriebswirtschaftlich richtiger Rechnung hohe Rückstellungen für spätere Jahre vorzunehmen wären!

Ich finde es gut, dass Du immer wieder auf die Notwendigkeiten der richtigen Kalkulation hinweist. Leider scheint es vielen SW einkommensmässig nicht möglich zu sein, angemessene Rücklagen zu bilden.

LG,
Friederike

[ehemaliger_User]

@Friederike

Es kann kein gerechtes Steuer- und Sozialsystem geben. Es wird immer ein jährlicher Schnappschuss der steuerlichen Leistungsfähigkeit gemacht. Der Versuch, das Steuersystem gerecht zu machen hat dazu geführt, unser System aufzublähen und Spezialisten Schlupflöcher aufzuzeigen. Oder es wurden extra Schlupflöcher geschaffen (Verlustzuweisungen)

Selbständige können Rückstellungen bilden, genauso wie jeder andere Betrieb auch: für künftig zu erwartenden Verpflichtungen, deren Höhe noch nicht fest steht. (Forderungsausfälle, Garantieleistungen, Entschädigungen...). Wird bei Sexdienstleistern aber schwierig (liegt an der Art der Arbeit).

Oder meinst Du Rücklagen? Rücklagen sind Eigenkapital, wird bei Kapitalgesellschaften gebildet. (Haftung!) Bei Personengesellschaften und Einzelunternehmer wegen der unbegrenzten Haftung der Eigner nicht nötig und operational unmöglich.

Seit 2011 können auch Betriebe keine steuermindernden Rücklagen z.B. für grössere Anschaffungen bilden.

Vorsorgeaufwendungen für den Aufbau einer Alters- oder Berufsunfähigkeitsversorgung können bis 20.000 EUR jährlich als Sonderausgaben geltend gemacht werden.

[Marc of Frankfurt]

Danke für diese Zahl:

Vorsorgeaufwendungen für den Aufbau einer Alters- oder Berufsunfähigkeitsversorgung können bis 20.000 EUR jährlich als Sonderausgaben geltend gemacht werden.

Das sind 1.600 Euro pro Monat

380 Euro pro Woche

50 Euro täglich

100 Euro je Arbeitstag (205 Arbeitstage/Jahr).


Gesamtkapital nach 10 Jahren Sexwork und regelmäßiger Einzahlung bei 5% Zinsen p.a.:
www.google.de/search?q=20000%281,05%5E1 ... 81,05-1%29
(Einfach mit anderen Zahlen überschreiben, um Varianten auszurechnen. Erklärung s.o. Seite 2, posting #34)

Mit 65 Jahren ein Vermögen von 111.000 € (Männer) und 131.000 € (Frauen) gespart zu haben, entspricht umgewandelt einer Rente bis zum Lebensende in Höhe von 647 €/Monat (absolute Armutsgrenze). Wer mehr benötigt muß den Rentenbetrag entsprechend multiplizieren, und mit dem selben Faktor das Vermögen, um das benötigte anzusparende Gesamtkapital zu ermitteln.


Beträge können unversteuert eingezahlt werden und müssen im Rentenalter bei Auszahlung gemeinsam mit den angefallenen Zinsen versteuert werden, wenn man höchstwahrscheinlich einen niedrigeren pers. Einkommensteuersatz hat.

Alterseinkünftegesetz:
http://de.wikipedia.org/wiki/Alterseink%C3%BCnftegesetz





Die Probleme, warum viele Sexworker es dennoch nicht so machen sind:

• Sexwork wird gesellschaftlich bedingt nicht als Berufskarriere empfunden (Stigma: "kein Beruf wie jeder andere" sagt die Ministerin). Selbst dann, wenn es später rückblickend doch eine Karriere im Sexbiz war, hat man nicht mehr zu korrigierende Fehler bereits beim Einstieg gemacht (fehlende, weil als "Förderung von Prostitution" verpönte Einstiegsberatung).
• Die Kultur der Sexarbeit entspricht psychologisch-emotional dem paradisisch-animalischen Naturzustand des Leben im "hier und jetzt" (Vergnügungsindustrie, Konzept: Privatheit, Sex, Liebe, Pretty-Women-Syndrom).
• In vielen Sexarbeitsbereichen wird einfach nicht genug verdient bezogen auf die gesellschaftlich nicht anerkannte harte Arbeit und langen Wartezeiten, so dass viele Sexarbeiter freiwillig zuzätzliche Abgaben nicht leisten wollen/können.
• Alleinselbstständige ohne entsprechende Ausbildung, Begleitung durch starke Berufsverbände oder Sexworker Akademie sind schlicht überfordert es richtig zu machen.
  
  "Altersvorsorge ist gemäß Lebenszyklustheorie ein intertemporales Maximierungsproblem zur Konsumglättung,
  welches rationale und vorausschauende Individum lösen müssen."
• Viele wollen nur kurzzeitig und diskret schnelles Geld machen... (private bail-out).

Der Grund für das berechtigte Sprichwort "Hurengut passt in einen Fingerhut" ist also zu einem Großteil strukturell bedingt, dadurch dass Sexworker aufgrund von Stigma, Tabu und Kriminalisierungen außerhalb der Gesellschaft stehen müssen. So entsteht quasi ganz automatisch die sog. "Falle Prostitution".





.

[friederike]

@ehemaliger_User,

was ich meine: eigentlich dürfte ein SW-Einkommen nicht in einem Jahr versteuert werden, wenn es denn gerecht zuginge, weil das Einkommen eben nicht konstant ist. Das Einkommen müsste als mehrjähriger Durchschnitt berücksichtigt werden.

Das geht über den Abzug für Altersvorsorge hinaus.

Eigentlich wäre also ein steuermindernder Abschlag, also quasi eine "Rückstellung" für Einkommensrückgang gerecht. Eine Rücklage muss dagegen aus dem Netto gebildet werden.

[Marc of Frankfurt]

Hier hat eine unabhängige Finanzberatung aus Bad Mergentheim viele kritische Insiderinfos zusammengestellt:

Altersvorsorge
www.besema.de/info-altersvorsorge.htm

Vermögensaufbau
www.besema.de/tipp-vermb1.htm

Inhalt
www.besema.de/sitemap.htm

[Marc of Frankfurt]

Finanzielles Berufswahl-Risiko Sexwork


Grundsätzliche Überlegungen zu:

• Einstieg in die Sexarbeit
• Verdienst in Lebenslaufbetrachtung
• Unternehmensführung
• Altersvorsorge
• Outplacement
• Marktwirtschaft
• Kostenübersicht in Lebenslaufbetrachtung (s.u.)

Ökonomische Orientierungshilfe mit vielen bunten Diagrammen und Schaubildern.


Erstmals 3D-Diagramm von Verdienst und Vermögen.

Auch ein Programm für weitere Sexwork-Forschung.

• Hier zum PDF-Download für nichtangemeldete User:
  
  "Zum finanziellen Berufswahl-Risiko Sexarbeit"
  
  PDF, 11 Seiten, 800 KB, mit vielen Schaubildern
  
  www.sexworker.at/phpBB2/download.php?id=904